How Do You Know What the Independent Variable Is in Linear Funtion

March 17, 2022 Post a Comment

Linear Regression and Correlation

Linear Equations

Linear regression for ii variables is based on a linear equation with one contained variable. The equation has the class:

$y=a+\text{bx}$

where a and b are constant numbers.

The variable x is the independent variable, and y is the dependent variable. Typically, you lot choose a value to substitute for the contained variable and so solve for the dependent variable.

The following examples are linear equations.

$y=3+\text{2x}$

$y=-0.01+\text{1.2x}$

Endeavour It

Is the following an example of a linear equation?

y = –0.125 – three.5x

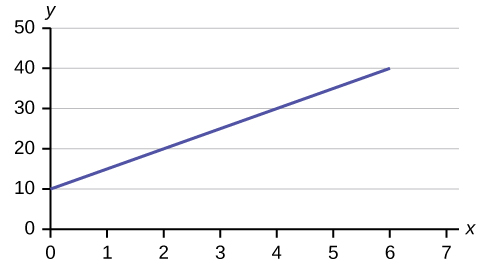
The graph of a linear equation of the form y = a + bx is a straight line. Any line that is not vertical tin be described by this equation.

Graph the equation y = –i + 2x.

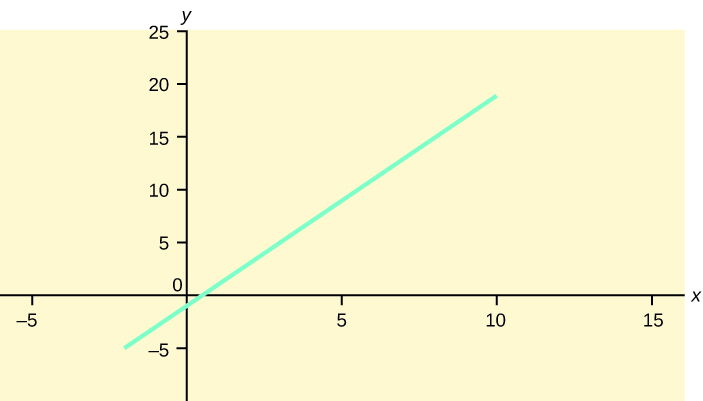
Graph of the equation y = -1 + 2x. This is a straight line that crosses the y-axis at -1 and is sloped up and to the right, rising 2 units for every one unit of run.

Try It

Is the following an case of a linear equation? Why or why not?

This is a graph of an equation. The x-axis is labeled in intervals of 2 from 0 - 14; the y-axis is labeled in intervals of 2 from 0 - 12. The equation's graph is a curve that crosses the y-axis at 2 and curves upward and to the right.

Aaron's Discussion Processing Service (AWPS) does word processing. The rate for services is ?32 per hour plus a ?31.fifty one-time charge. The total cost to a customer depends on the number of hours information technology takes to complete the job.

Find the equation that expresses the full cost in terms of the number of hours required to consummate the job.

Permit x = the number of hours information technology takes to get the chore washed.
Let y = the full cost to the customer.

The ?31.50 is a fixed cost. If it takes 10 hours to consummate the job, so (32)(10) is the cost of the give-and-take processing merely. The full cost is: y = 31.fifty + 32x

Try It

Emma's Extreme Sports hires hang-gliding instructors and pays them a fee of ?50 per class likewise as ?20 per student in the class. The full cost Emma pays depends on the number of students in a grade. Observe the equation that expresses the total cost in terms of the number of students in a grade.

Slope and Y-Intercept of a Linear Equation

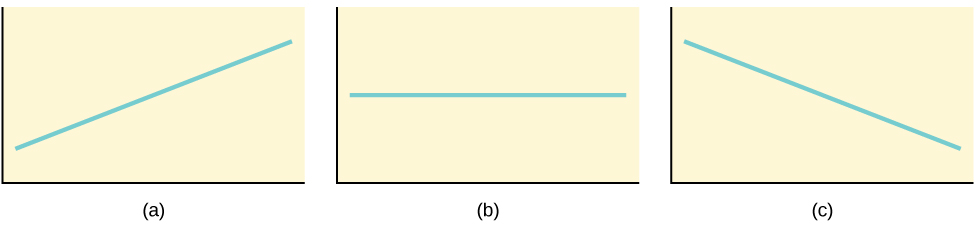
For the linear equation y = a + bx, b = slope and a = y-intercept. From algebra think that the slope is a number that describes the steepness of a line, and the y-intercept is the y coordinate of the point (0, a) where the line crosses the y-axis.

Three possible graphs of y = a + bx. (a) If b > 0, the line slopes upwardly to the correct. (b) If b = 0, the line is horizontal. (c) If b < 0, the line slopes down to the right.

Three possible graphs of the equation y = a + bx. For the first graph, (a), b > 0 and so the line slopes upward to the right. For the second, b = 0 and the graph of the equation is a horizontal line. In the tertiary graph, (c), b < 0 and the line slopes downward to the right.

Svetlana tutors to make actress money for college. For each tutoring session, she charges a erstwhile fee of ?25 plus ?15 per hour of tutoring. A linear equation that expresses the total amount of money Svetlana earns for each session she tutors is y = 25 + fifteenx.

What are the contained and dependent variables? What is the y-intercept and what is the slope? Interpret them using complete sentences.

The contained variable (x) is the number of hours Svetlana tutors each session. The dependent variable (y) is the corporeality, in dollars, Svetlana earns for each session.

The y-intercept is 25 (a = 25). At the beginning of the tutoring session, Svetlana charges a one-fourth dimension fee of ?25 (this is when x = 0). The slope is 15 (b = 15). For each session, Svetlana earns ?15 for each hr she tutors.

Try Information technology

Ethan repairs household appliances like dishwashers and refrigerators. For each visit, he charges ?25 plus ?twenty per hour of work. A linear equation that expresses the total amount of coin Ethan earns per visit is y = 25 + twentyx.

What are the contained and dependent variables? What is the y-intercept and what is the gradient? Interpret them using complete sentences.

Affiliate Review

The most basic blazon of association is a linear association. This type of relationship can be defined algebraically past the equations used, numerically with actual or predicted data values, or graphically from a plotted curve. (Lines are classified as straight curves.) Algebraically, a linear equation typically takes the form y = mx + b , where g and b are constants, ten is the independent variable, y is the dependent variable. In a statistical context, a linear equation is written in the form y = a + bx , where a and b are the constants. This form is used to help readers distinguish the statistical context from the algebraic context. In the equation y = a + bx, the constant b that multiplies the 10 variable (b is chosen a coefficient) is called as the slope. The gradient describes the rate of change between the independent and dependent variables; in other words, the rate of change describes the change that occurs in the dependent variable as the independent variable is changed. In the equation y = a + bx, the constant a is called as the y-intercept. Graphically, the y-intercept is the y coordinate of the point where the graph of the line crosses the y axis. At this betoken 10 = 0.

The slope of a line is a value that describes the rate of change between the contained and dependent variables. The gradient tells us how the dependent variable (y) changes for every one unit increment in the independent (x) variable, on average. The y-intercept is used to describe the dependent variable when the independent variable equals zip. Graphically, the slope is represented by three line types in elementary statistics.

Formula Review

y = a + bx where a is the y-intercept and b is the gradient. The variable x is the independent variable and y is the dependent variable.

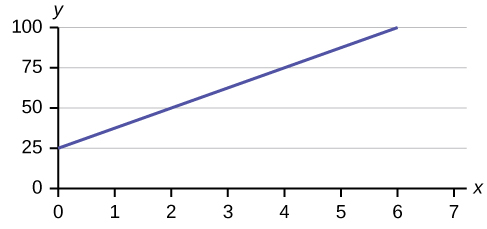
Utilize the following data to respond the next three exercises. A vacation resort rents SCUBA equipment to certified divers. The resort charges an upward-front fee of ?25 and another fee of ?12.50 an hour.

What are the dependent and independent variables?

dependent variable: fee amount; independent variable: time

Discover the equation that expresses the total fee in terms of the number of hours the equipment is rented.

Graph the equation from (Effigy).

This is a graph of the equation y = 25 + 12.50x. The x-axis is labeled in intervals of 1 from 0 - 7; the y-axis is labeled in intervals of 25 from 0 - 100. The equation's graph is a line that crosses the y-axis at 25 and is sloped up and to the right, rising 12.50 units for every one unit of run.

Utilise the following information to answer the next ii exercises. A credit menu company charges ?ten when a payment is late, and ?five a solar day each solar day the payment remains unpaid.

Observe the equation that expresses the full fee in terms of the number of days the payment is late.

Graph the equation from (Figure).

This is a graph of the equation y = 10 + 5x. The x-axis is labeled in intervals of 1 from 0 - 7; the y-axis is labeled in intervals of 10 from 0 - 50. The equation's graph is a line that crosses the y-axis at 10 and is sloped up and to the right, rising 5 units for every one unit of run.

Is the equation y = ten + 5x – 3x ² linear? Why or why non?

Which of the following equations are linear?

a. y = 6x + viii

b. y + seven = 310

c. y – x = viiiten ^two

d. 4y = 8

y = 6x + 8, 4y = 8, and y + seven = 3ten are all linear equations.

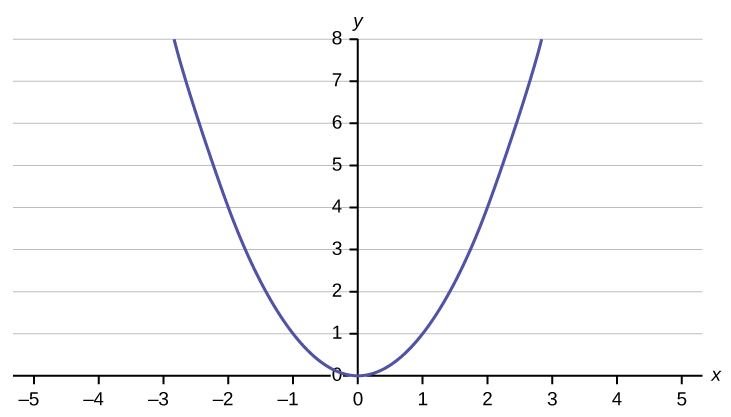
Does the graph prove a linear equation? Why or why not?

This is a graph of an equation. The x-axis is labeled in intervals of 1 from -5 to 5; the y-axis is labeled in intervals of 1 from 0 - 8. The equation's graph is a parabola, a u-shaped curve that has a minimum value at (0, 0).

(Effigy) contains real data for the first ii decades of flu reporting.

Adults and Adolescents simply, United States
Twelvemonth	# influenza cases diagnosed	# flu deaths
Pre-1981	91	29
1981	319	121
1982	i,170	453
1983	3,076	i,482
1984	half-dozen,240	3,466
1985	11,776	6,878
1986	19,032	11,987
1987	28,564	16,162
1988	35,447	20,868
1989	42,674	27,591
1990	48,634	31,335
1991	59,660	36,560
1992	78,530	41,055
1993	78,834	44,730
1994	71,874	49,095
1995	68,505	49,456
1996	59,347	38,510
1997	47,149	20,736
1998	38,393	19,005
1999	25,174	18,454
2000	25,522	17,347
2001	25,643	17,402
2002	26,464	16,371
Total	802,118	489,093

Apply the columns "year" and "# flu cases diagnosed. Why is "twelvemonth" the contained variable and "# influenza cases diagnosed." the dependent variable (instead of the contrary)?

The number of flu cases depends on the year. Therefore, year becomes the independent variable and the number of influenza cases is the dependent variable.

Use the post-obit data to answer the next two exercises. A specialty cleaning company charges an equipment fee and an hourly labor fee. A linear equation that expresses the total corporeality of the fee the visitor charges for each session is y = 50 + 10010.

What are the independent and dependent variables?

What is the y-intercept and what is the slope? Interpret them using consummate sentences.

The y-intercept is 50 (a = l). At the start of the cleaning, the company charges a ane-fourth dimension fee of ?50 (this is when x = 0). The gradient is 100 (b = 100). For each session, the company charges ?100 for each hour they clean.

Use the following data to answer the side by side three questions. Due to erosion, a river shoreline is losing several chiliad pounds of soil each twelvemonth. A linear equation that expresses the total amount of soil lost per year is y = 12,000x.

What are the independent and dependent variables?

How many pounds of soil does the shoreline lose in a year?

12,000 pounds of soil

What is the y-intercept? Translate its meaning.

Use the following information to respond the next two exercises. The price of a single issue of stock can fluctuate throughout the mean solar day. A linear equation that represents the price of stock for Shipment Express is y = 15 – 1.fivex where x is the number of hours passed in an eight-hour 24-hour interval of trading.

What are the slope and y-intercept? Translate their meaning.

The slope is –one.5 (b = –1.5). This means the stock is losing value at a charge per unit of ?ane.50 per 60 minutes. The y-intercept is ?fifteen (a = 15). This means the price of stock before the trading mean solar day was ?15.

If you lot owned this stock, would you want a positive or negative slope? Why?

Homework

For each of the post-obit situations, state the independent variable and the dependent variable.

A study is washed to determine if elderly drivers are involved in more motor vehicle fatalities than other drivers. The number of fatalities per 100,000 drivers is compared to the age of drivers.
A study is done to determine if the weekly grocery bill changes based on the number of family members.
Insurance companies base life insurance premiums partially on the age of the applicant.
Utility bills vary according to power consumption.
A study is done to determine if a higher education reduces the crime rate in a population.

independent variable: age; dependent variable: fatalities
contained variable: # of family members; dependent variable: grocery bill
independent variable: historic period of bidder; dependent variable: insurance premium
independent variable: ability consumption; dependent variable: utility
independent variable: higher education (years); dependent variable: criminal offense rates

Piece-rate systems are widely debated incentive payment plans. In a recent study of loan officer effectiveness, the post-obit piece-rate system was examined:


% of goal reached	< 80	80	100	120
Incentive	n/a	?4,000 with an additional ?125 added per percentage signal from 81–99%	?vi,500 with an additional ?125 added per percentage betoken from 101–119%	?9,500 with an boosted ?125 added per per centum point starting at 121%

If a loan officeholder makes 95% of his or her goal, write the linear function that applies based on the incentive plan table. In context, explain the y-intercept and gradient.

martinnowityriet.blogspot.com

Source: https://opentextbc.ca/introstatopenstax/chapter/linear-equations/